인덱스 순차 파일 구조는 파일이 커질수록 인덱스를 찾아서 그 데이터를 연속으로 스캔하는 성능이 감소한다는 것이다. B+-tree index 구조는 데이터 삽입, 삭제에 상관없이 성능을 유지하는 인덱스 구조 중 가장 널리 사용된다. B+-tree index는 root에서 leaf node까지 모든 경로의 길이가 같은 balanced tree이다. 이 때문에 검색, 삽입, 삭제 성능이 좋다. B+-tree에서는 Root node를 제외한 다른 노드들이 n/2~n 사이의 자식을 갖고, root는 2~n개 사이의 자식을 갖는다.
B+-tree 구조
B-+tree index는 다계층 인덱스이지만 다계층 인덱스 순차 파일과는 다른 구조를 가진다. 아래 설명에선 우선 각 검색 키가 고유하다는 전제하에 B+-tree index를 설명한다.
B+-tree index의 노드는 다음과 같이 n-1 개의 검색 키값 (k1~kn-1)과 n개의 포인터(p1~pn)을 포함한다. 노드 안에 검색 키값은 정렬된 순서를 유지한다.
이런 구조를 가진 leaf node의 포인터 Pi(i 범위: 1~n-1)는 검색 키 값 Ki에 대한 파일 레코드를 가리킨다. n=4 일때의 leaft node 구조는 다음과 같다.
Li와 Lj가 leaf node이고, i < j 이면 Li에 있는 모든 검색 키 값은 Lj에 있는 모든 검색 키 값보다 작다. 만약 B+-tree index가 dense index로 사용된다면, leaf node에 모든 검색 키 값이 존재해야 한다.
위 설명에서 leaf node는 n개의 포인터를 가진다고 설명했다. 그중 n번째 포인터인 pn은 leaft node를 검색 키 순서로 서로 연결하기 위해 사용된다. 각 leaf node는 검색 키 값을 기초로 선형 순서로 되어있기 때문이다.
B+-tree의 비단말 노드(nonleaf node, 내부 노드 - internal node)는 leaf node상에서 다계층(sparse) 인덱스를 형성한다. nonleaf node는 모든 포인터가 기타 트리 노드를 가리킨다는 것을 제외하면 leaf node와 구조가 같다. 한 노드의 포인터 수를 그 노드의 팬아웃(fanout)이라 한다.
m (m <= n)의 포인터를 포함하는 노드가 있다고 해보자. 1 <= i <= m-1 일 때, 포인터 pi가 가리키는 서브 트리 검새 키 값 범위는 (ki, ki-1]이다. 포인터 pm은 km-1보다 크거나 같은 기 값을 포함하는 서브 트리 가리킨다. 포인터 p1은 k1보다 작은 검색 키 값을 포함하는 서브 트리를 가리킨다. 전체적으로 B+-tree는 다음과 같은 구조를 가진다.
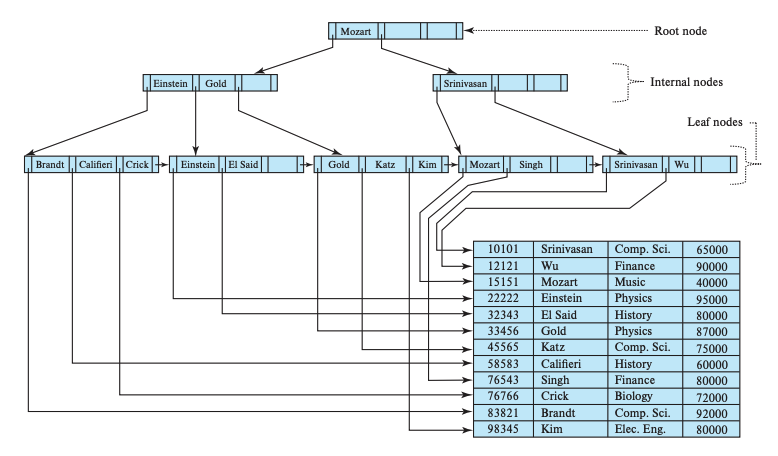검색 키는 중복된 값을 가질 수 있다. 중복된 검색 키를 구현하기 위해 leaf node에 중복된 횟수만큼 동일한 검색 키를 저장한다거나 secondary index처럼 버켓을 사용하면 삽입, 삭제에 많은 비용이 필요하다. 따라서 고유하지 않은 검색 키를 고유한 검색 키와 묶어서 고유하게 만들어 사용한다. 테이블 r의 검색 키 d가 고유하지 않다고 해보자. r의 pk를 u라고 해보자. 그러면 인덱스 구축 시 복합 검색키로 (d, u)를 사용한다.
B+-tree 질의
검색 키 값 v를 가진 모든 레코드를 찾는 의사 코드 find(v) 함수는 다음과 같다. 검색 키 값은 고유하며, 검색 키와 레코드가 1:1 매핑된다고 가정한다.
단일 검색 키 탐색
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function find(searchKey) {
Set currentNode = root node // 루트부터 시작해 아래 방향으로 탐색한다.
// 현재 노드를 조사해 searchKey 값보다 큰 검색 키 Ki를 만족하는 i를 찾는다.
while (currentNode is not a leaf node) begin
Let i = smallest number such that searchKey <= currentNode.Ki
// searchKey > Km-1, Pm은 node의 마지막 포인터(같은 계층에서 다음 노드를 가르킨다)
if there is no such number i then begin
Let Pm = last non-null pointer in the node
Set currentNode = currentNode.Pm
end
// if를 거치면 필요한 값 i가 발견되었다는 의미
// searchKey와 currentNode.Ki 관계에 따라 currentNode 이동
else if (searchKey = currentNode.Ki) then Set currentNode = currentNode.Pi+1
else Set currentNode = currentNode.Pi // searchKey < currentNode.Ki
end
// currentNode is a leaf node
if for some i, Ki = searchKey
then return Pi // Ki와 searchKey가 같으면 Pi가 원하는 레코드를
else return null; // No record with key value v exsits
}
범위 탐색
B+-tree는 특정 범위의 검색 키 값을 가지는 모든 레코드를 찾기 위해 사용할 수 있다. 이런 쿼리를 range query라 한다. 검색 키를 기준으로 특정 범위에 대한 모든 레코드를 찾는 의사 코드 findRange(lowerBound, upperBound)는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
function findRange(lowerBound, upperBound) {
// Returns all records with serach key value searchKey such that lowerBound <= searchKey <= upperBound
Set resultSet = {};
Set currentNode = root node
// 위의 단일 검색 키 탐색과 비슷한 방식으로 leaft node로 이동한다.
// leaf node는 lowerBound를 포함하지 않을 수도 있다
while (currentNode is not a leaf node) begin
Let i = smallest number such that lowerBound <= currentNode.Ki
if there is no such number i then begin
Let Pm = last non-null pointer in the node
Set currentNode = currentNode.Pm
end
else if (lowerBound = currentNode.Ki) then Set currentNode = currentNode.Pi+1
else Set currentNode = currentNode.Pi // lowerBound < currnetNode.Ki
end
// currentNode is a leaf node
Let i be the least value such that Ki >= lowerBound
if there is no such i
then Set i = 1 + number of keys in currnetNode; // To force move to nest leaf
Set done = false;
// 찾은 leaf node와 뒤따라오는 leaf node들을 모두 검사한다.
while (node done) begin
Let n = number of keys in currentNode
// lowerBound <= node인 조건으로 해당 반복문을 시작했으므로
// 이 조건문은 lowerBound <= currneNode.Ki <= upperBound와 같다.
// 즉, 범위 내에 있는 값의 조건이다.
if (i < n and currnetNode.Ki <= upperBound) then begin
Add currentNode.Pi to resultSet
Set i = i + 1
end
// 범위 초과, 반복문 종료
else if (i <= n and currentNode.Ki > upperBound)
then Set done = true;
// 더 탐색할 노드가 남아있는 경우
else if (i > n and currentNode.Pn+1 is not null)
// move to next leaf
then Set currentNode = currentNode.Pn+1 and i = 1
// No more leaves to the right
else Set done = true;
end
return resultSet;
}
B+-tree index에 대한 쿼리 비용은 최악의 경우 경로 길이는 logn/2(N) 이다(n은 트리 레벨 하나에서 포함할 수 있는 최소한의 레코드 개수, N은 파일의 전체 레코드 개수). B+-tree와 binary tree의 차이는 노드 크기와 그로 인한 트리 높이에 있다. binary tree는 각 노드가 작고, 많아야 두 개의 포인터를 갖는다. 그에 반해 B+-tree는 일반적으로 디스크 블록 크기만큼의 크기를 갖는다. 또한, 각 노드는 많은 양의 포인터를 가질 수 있다. 이로 인해 B+-tree index는 일반 Balanced binary tree보다 더 적은 블록을 읽고 원하는 레코드를 찾을 수 있다. 예컨대, 검색 키 크기가 32byte, 디스크 포인터 크기가 8byte, disk block이 4,000byte인 상황에서 파일 전체 레코드 개수 N이 1,000,000이라 하자. Balanced binary tree는 검색을 위한 경로 길이가 log2(N)이므로 20개의 노드에 접근해야 한다. 반면 B+-tree는 n(트리 레벨 하나가 포함해야 하는 최소한의 레코드 개수)은 디스크 블록 크기 / (인덱스 노드 크기(검색 키 크기 + 디스크 포인터 크기)) = 4,000 / (32 + 8) = 100(대략적 수치)이다. 따라서 log50(1,000,000) = 4 이다. 디스크는 암 탐색과 블록을 읽는데 통상적으로 10ms를 소요하기 때문에 B+-tree를 사용하는 편이 훨씬 효율적이다. 플래시 저장 장치는 4KB 블록을 읽는데 10~100μs가 소요돼서 시간이 더 적게 걸리지만, 여전히 차이는 존재한다. 이제 leaf node에 도착한 뒤 검색 키와 일치하는 레코드를 가져오는 비용을 고려해 보자.
- 범위 탐색 쿼리
- leaf node에 도착한 뒤, 주어진 범위 내에 있는 모든 포인터를 검사해야 한다. 검색할 포인터가 총 M개 이면 M/(n/2)+1(각 노드는 최소 n/2개의 포인터가 존재한다.)개 단말 노드에 접근하는 비용과 실제 레코드에 접근하는 비용이 필요하다.
- secondary index
- 각 레코드가 서로 다른 블록에 위치할 수 있다. M개의 I/O 발생
- Clustering index
- 레코드는 연속된 블록에 위치해 있으며, 각 블록에는 여러 개의 레코드가 포함되어 있어서 비용이 절감된다.
B+-tree 갱신
B+-tree 삽입과 삭제는 탐색보다 더 복잡한 연산이 필요하다. B+-tree 특징을 유지하면서 삽입과 삭제를 해야 하기 때문이다. 때문에 노드 하나를 경우에 따라 분리하거나, 노드들을 합치는 경우가 존재한다. 노드가 분리, 결합되지 않는다고 가정하면 삽입과 삭제 과정은 다음과 같이 단순화된다.
- 삽입
- 위에서 설명한 단일 검색 키 탐색의 find()와 같은 방식으로 검색 키값이 있는 leaf node를 찾는다. 그 후, leaf node에 있는 엔트리를 삽입하면서 검색 키의 순서를 유지하게 조정한다.
- 삭제
- 이 역시 find()와 같은 방식으로 삭제될 엔트리를 포함하는 leaf node를 찾는다. 만약 검색 키 값을 가지는 다중 엔트리가 존재한다면, 삭제될 레코드를 가리키는 엔트리를 찾을 때까지 같은 검색 키 값을 가지는 모든 엔트리를 검색한다. 찾은 엔트리를 제거하고, leaf node에 있는 삭제된 엔트리 오른쪽에 있는 모든 엔트리를 왼쪽으로 이동시킨다.
B+-tree 갱신은 연산과정 자체는 복잡하지만 상대적으로 적은 디스크 I/O 연산을 요구한다. 삽입의 경우 최악의 경우 logn/2(N), 삭제의 경우 검색 키에 대한 중복이 없다는 전제하에 logn/2(N)이다. (N은 인덱스된 파일에 있는 레코드 개수, n은 노드 하나에 있는 포인터 최대 개수). 즉, 갱신 비용은 B+-tree 높이에 비례한다. 이렇게 적은 디스크 I/O 연산은 B+-tree index를 사용하는 주된 이유이다.
비고유 검색 키
위의 설명들은 모두 검색 키가 고유하다는 전제하에 진행되었다. 또 한, 검색 키가 고유하지 않다면 추가 속성을 함께 사용해 모든 레코드가 고유한 복합 검색 키를 사용하게 한다고 설명했다. 이때 사용하는 추가 속성은 record-id(레코드에 대한 포인터), pk 또는 동일한 검색 키값을 가진 모든 레코드 사이에서 값이 고유한 속성일 수 있다. 이런 추가 속성을 고유자(uniquifier)라고 한다. 이런 방식을 사용하지 않고, 비고유 검색 키를 그대로 사용한다면 다음과 같은 방법을 고려할 수 있다.
- 원래 검색 키 속성에 대해 범위 검색을 수행한다.
- 원래 검색 키 값만 매개변수로 사용해 검색 키 값을 비교할 때 고유자 속성값을 무시하게 findRang() 코드를 변경한다
- 중복 검색 키를 지원하게 B+-tree 구조는 수정한다. 그에 따라 삽입, 삭제, 검색 방법도 수정한다.
위 방법 중 B+-tree 구조 수정을 원치 않는다면 다음과 같은 대안들도 존재한다.
- 각 키 값을 트리에 한 번만 저장하고, 비고유 검색 키를 다루기 위한 검색 키 값과 레코드 포인터를 담는 버켓을 유지한다.
- 이 방식에서 버켓을 leaf node에 저장한다면, 가변 크기 버켓을 처리하고 leaf node보다 커지는 버켓을 다루기 위한 추가 코드가 필요하다.
- 버켓을 블록에 저장한다면 레코드를 가져오기 위한 추가 I/O가 발생한다.
- 레코드마다 검색 키 값을 저장한다.
- 두 leaf node에 동일한 검색 키 값이 존재할 수 있기에 내부 노드의 분할, 검색 처리가 더 복잡해진다. 또 한, 키 값이 해당 값을 포함하는 레코드 수만큼 저장되어 오버헤드가 발생한다.
이렇게 비고유 검색 키를 사용한다면 삭제 효율이 저하된다. 특정 검색 키 값이 여러 개 존재하고, 해당 검색 키 값을 가지는 레코드가 삭제된다면, 레코드에 해당하는 엔트리를 찾기 위해 여러 단말 노드에서 동일한 검색 키 값을 가진 여러 엔트리를 검색해야 한다. 최악의 경우 레코드 수에 비례하는 삭제 복잡도를 가진다. 반면 검색 키가 고유하다면 위에서 설명한 바와 같이 삭제가 레코드 수의 로그값에 비례한다. 이 때문에 대부분의 DB 시스템의 B+-tree 구현은 고유한 검색 키만 다루고, 비고유 검색 키를 고유하게 만들어 사용한다.
B-tree index file
B-tree index와 B+-tree index의 가장 큰 차이는 B-tree index는 검색 키 값이 트리상에서 고유하다는 것이다. 위에 있는 B+-tree index 예시에서 Mozart라는 이름이 root node와 leaf node에 모두 존재한다. 그러나 B-tree index는 비단말 노드에 각 검색 키를 위한 부갖거인 포인터 필드를 포함하고, 이 포인터 필드가 파일 레코드나 관련된 검색 키를 위한 버켓을 가리킨다. 때문에 검색 키 값이 트리상에서 고유하다.
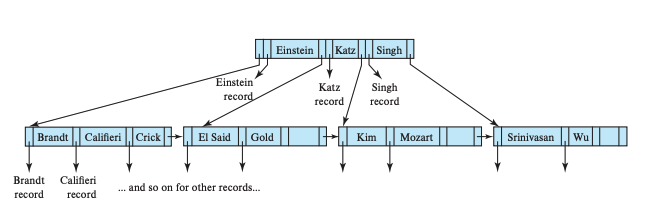이런 특성 때문에 leaf node에 도달하기 전에 원하는 값을 찾을 가능성이 존재해 검색 시 접근되는 노드 수는 검색 키 위치에 달려있다. 그러나 B-tree의 leaf node는 비단말 노드보다 약 n배 많은 키를 저장하고 있고, n배는 큰 값이기에 값을 빨리 찾음으로 인한 이익은 줄어든다. 또 한, 비단말 노드가 B+-tree에 비히 적은 검색 키를 가지고 있어서 B-tree index 높이가 더 높을 수도 있다. 때문에 일부 검색 키에 대한 탐색을 제외하면 다른 검색 키를 찾는 속도가 B+-tree보다 더 느리다.
B-tree index는 B+-tree index와 달리 비단말 노드에서도 삭제가 발생할 수 있기 때문에 삭제 로직이 더 복잡하다.
B-tree가 가지는 공간적 이득 또한 큰 인덱스에서는 큰 의미가 없다. 때문에 B-tree보다는 B+-tree가 더 많이 사용된다.