Multiplexer (Mux)
복수의 정보가 있고, 그중 적용할 것을 선택해야 할 때 사용하는 회로입니다. 멀티플렉서에는 2^n 개의 입력, n개의 선택선과 하나의 출력을 가집니다.
2:1 멀티플렉서의 경우다음과 같이 표시할 수 있고 진리표는 다음과 같습니다.
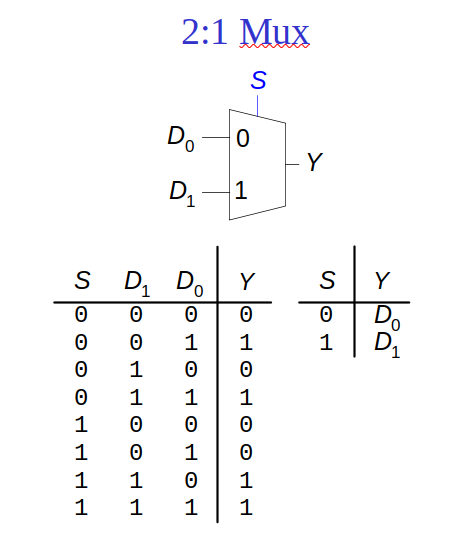위 진리표를 통해 카르노맵을 다음과 같이 그릴 수 있습니다.
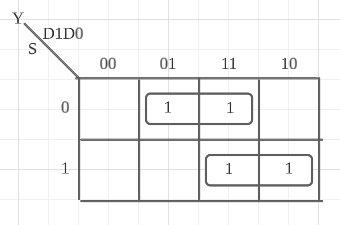이를 통해 그린 2:1 MUX 회로도는 다음과 같습니다.
Decoder
특정 입력 비트에 대해 특정 출력만 활성화되는 기능이 필요할 때 사용합니다. 한 번에 하나의 출력만 활성화됩니다.
n 개의 입력에 대해 2n 개의 출력이 존재하므로 2:4 decoder는 다음과 같이 표시할 수 있습니다.
이 역시 각 Y에 대해 카르노맵을 그리고 최종적으로 회로를 그릴 수 있습니다.
우선 각 Y에 대한 카르노맵은 다음과 같습니다.
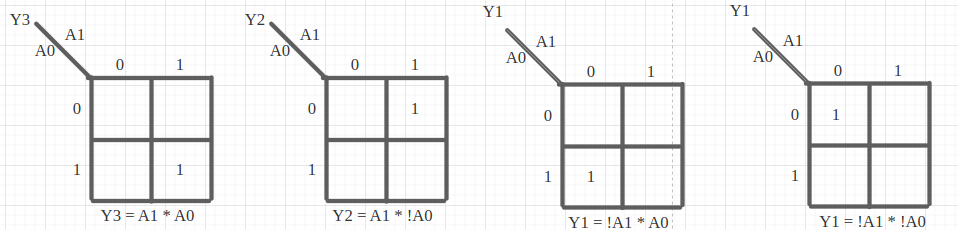회로는 다음과 같습니다.
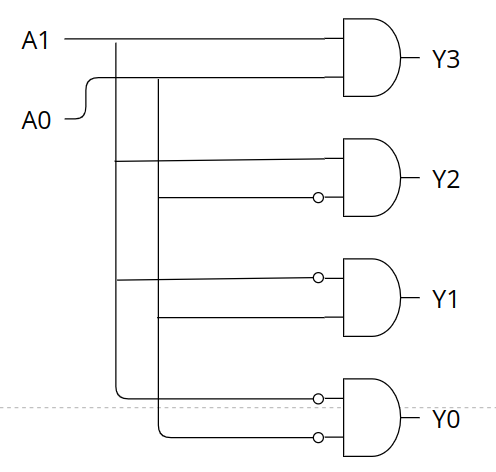
1-bit Adder
두 개의 비트를 더해서 값을 산출할 때 사용합니다. 가산기에는 오버플로를 위한 Cout(Carry out)과 두 비트 입력을 가진 반가산기(Half adder)와 carry를 받아 입력으로 사용하는 전가산기(full adder)가 있습니다.
각 출력에 대한 수식이 존재하므로 바로 회로를 그려볼 수 있습니다.
반가산기 회로도는 다음과 같습니다.
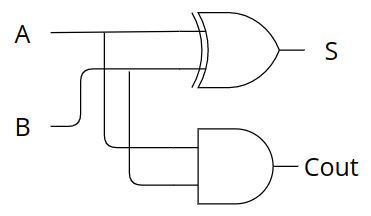전가산기 회로도는 다음과 같습니다.
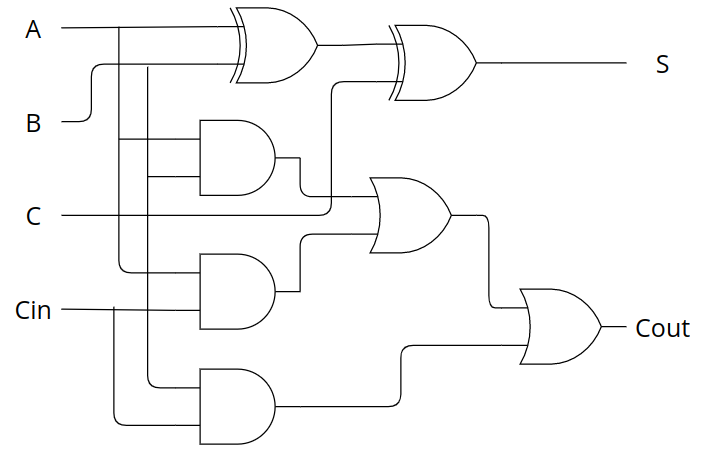만약 n-bit adder가 필요하다면 위에서 설명한 full adder를 n 개 이어붙이면 됩니다. 이를 Ripple-Carry Adder라 합니다.
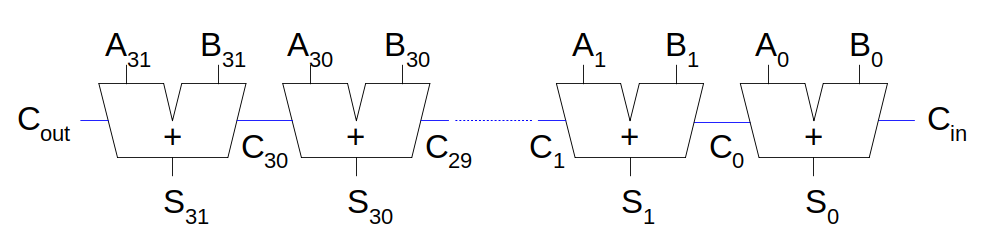하지만 Riplle-Carry Adder는 비트 수가 늘어남에 따라 연산 횟수가 증가하므로 느리다는 단점이 있습니다. 이를 극복하고자 하드웨어 자원을 더 많이 사용해 속도를 올린 것이 Carry-lookahead adder와 Prefix adder입니다. 이들의 심볼은 다음과 같습니다.
R-S Latch
위에서 살펴본 회로들은 연산을 수행할 뿐, 연산 결과를 기억하지 못합니다. 따라서 데이터를 기억할 수 있는 회로가 필요한데 그중 하나가 래치입니다. 래치는 비트 하나를 저장하며 Reset과 Set이 입력으로 주어지는 래치를 R-S Latch입니다. R-S Latch는 NOR 게이트를 활용해 구현하는 방식과 NAND를 활용해 구현하는 두 가지 방식이 존재합니다. 우선 NOR 게이트를 활용한 R-S Latch를 살펴본 뒤 이를 통해 NAND 게이트를 활용한 회로도를 도출하겠습니다.
NOR형 R-S Latch
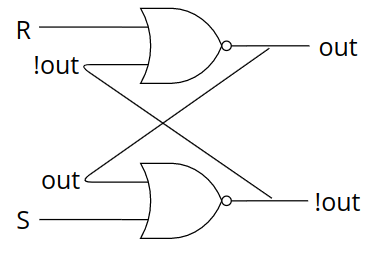
위 진리표에서 살펴볼 수 있듯이 S, R이 모두 0이면 상태를 유지하므로 비트를 저장할 수 있습니다. 만약 저장된 비트를 바꾸어야 한다면 R 또는 S를 1로 바꾸면 됩니다.
여기서 주의할 점이 R과 S는 동시에 1이 될 수 없다는 것입니다. 그 이유는 R과 S가 모두 1일 때 나올 수 없는 값이 출력되기 때문입니다. 예를 들어 S = 1, R = 1, out1(첫 번째 out) = 1, !out1 = 0이라면 R NOR !out1(1 NOR 1) = 0, S NOR out1(1 NOR 0) = 0이 됩니다. out1 = 0, !out1 = 1인 상황에서도 R NOR !out(1 NOR 1) = 0, S NOR out(1 NOR 0) = 0이 됩니다. out == !out == 0인 상황이 발생하므로 나올 수 없는 값이 나옵니다.
NAND형 R-S Latch
이제 NOR형 R-S Latch를 통해 NAND형 R-S Latch를 만들어 보겠습니다. 우선 NOR gate의 진리표는 다음과 같습니다.
NOR 게이트의 진리표를 보면 결과가 AND 게이트의 입력을 NOT 연산 수행한 것과 같다는 것을 알 수 있습니다.
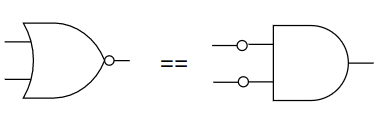따라서 NOR형 R-S Latch를 다음과 같이 변경할 수 있습니다.
이제 NOT의 위치를 조금 바꾸어 보겠습니다. R, S 입력이 NOT이 된 채로 입력으로 들어온다고 가정하면 R, S에 해당하는 NOT을 없앨 수 있습니다. 또 한, !out, out 입력에 대한 NOT은 출력 위치로 옮긴다면 결과의 변화 없이 NAND를 사용한 R-S Latch로 변환할 수 있습니다.
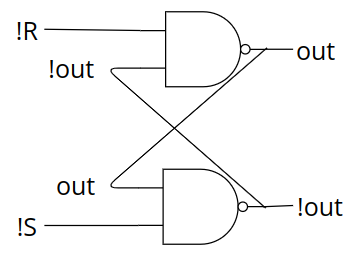마지막으로 !R을 R로, !S를 S로 표현하면 됩니다
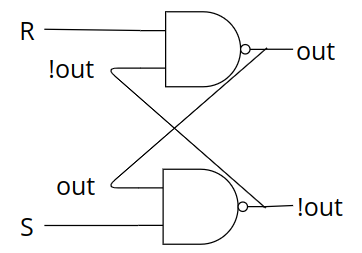NAND형 R-S Latch의 진리표는 다음과 같습니다.
