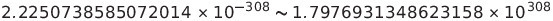2진수로 소수를 표현하는 방법으로는 고정소수점(fixed-point format)과 부동소수점(fixed-point notation)이 존재한다.
고정 소수점(fixed-point format)
특정 비트부터 소수점으로 사용할 수 있게 소수점 위치가 정해진 방식을 의미한다. 고정소수점 방식은 정수부와 소수점 아래를 표현하는 소수점 이하로 나눠져 있다. 이 방식은 비트에서 소수점을 표현하는 위치가 정해져 있기 때문에 수를 크게 만들거나 너무 작은 수를 표현해야 한다면 할당된 메모리 한계로 표현이 불가능해진다. 이 문제를 해결한 것이 부동소수점이다.
부동소수점(floating-point notation)
부동 소수점을 컴퓨터에서 사용하기 위해 과학적 표기법을 이용한 이진수를 사용한다.
과학적 표기법(scientific notation)
과학적 표기법(scientific notation)은 매우 큰 수나 매우 정밀한 소수점을 표현할 때 사용하는 방식이다. 예를 들어 0.00000000026을 과적적 표기법으로 표현하면 2.6 x 10^(-10)이 된다.
과학적 표기법을 일반화하면 다음과 같다.
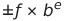
여기서 f를 가수, b를 밑, e를 지수라 한다.
2진수 과학적 표기법은 10진수 과학적 표기법과 상당이 유사하다. 2진수 과학적 표기법은 10진수와 마찬가지로 소수점 아래 자리를 2에 대한 음의 거듭제곱으로 표현한다.
|
1
2
3
|
101.1101 = 1x2^2 + 0x2^1 + 1x2^0 + 1x2^(-1) + 1x2^(-2) + 0x2^(-3) + 1x2^(-4)
= 1x4 + 0x2 + 1x1 + 1x0.5 + 1x0.25 + 0x0.125 + 1x0.0625
= 5.8125(10)
|
cs |
10진수 표기법에서 정규화된 가수부를 X라 하면, 가수부 범위가 1 <=X <10 이듯, 2진수 과학적 표기에서도 정규화된 가수부를 BX라 하면 범위는 1(2)<=BX <10(2)이 된다.
정규화된 부동소수점 수의 가수부에서 소수점 윗자리의 수는 항상 1이다. 이러한 표준은 IEEE 754 - 2008에 정의돼 있다.
IEEE 표준에서는 소수점을 표현하는 방식 중 4byte를 사용하는 단정도(single precision) 형식과 8byte를 사용하는 배정도(double precision) 두 가지 기본 형태가 정의돼 있다.
단정도 표기법(single precision)
단정도 형식은 다음과 같은 구조로 이루어져 있다.
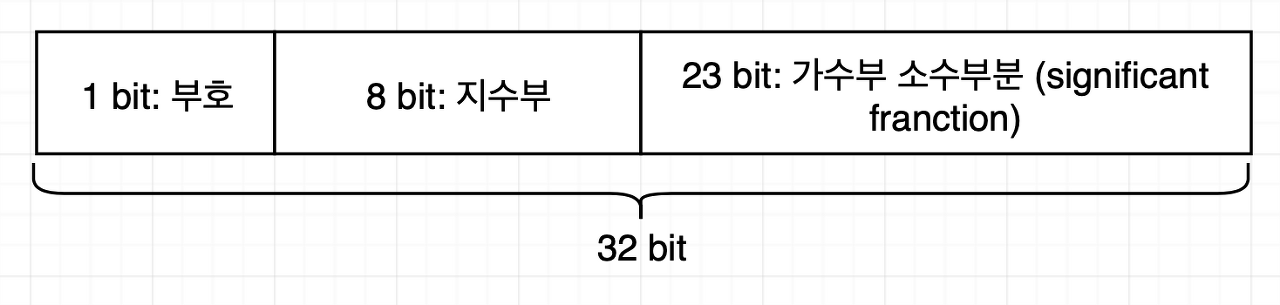
위 구조에서 가수부는 정규화된 2진 부동소수점이다. 따라서 소수점 앞에 항상 1의 값을 가진다. IEEE 형식에서 부동소수점 수를 저장할 때는 이 값을 포함하지 않는다. 따라서 가수부는 23bit이지만 정밀도는 24bit이다. 8bit 지수부는 0~255까지의 값을 가진다. 이 지수부는 편향된 지수(biased exponent)이다. 이는 설정된 값에서 편중치(bias)를 빼서 실제로 적용한 지수값을 산출하는 방식이다. 단정도 표기법에서 부동소수점 편중 치는 127이다.
위 서술을 식으로 표현하면 다음과 같다.
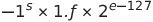
여기서 s가 0이면 값이 양수고, s가 1이면 값이 음수다. f는 23bit 가수 부이고 e-127은 8bit 크기의 편향된 지수이며 127을 빼서 계산한다. 8bit 지수부 범위 중 0과 255는 다음과 같이 특수한 용도로 사용된다.
- e=0 AND f=0 이면 값이 0이다.
- e=0 AND f!=0 이면 유효한 수이지만 정규화가 되지 않은 수다.
- e=255 AND f-0 이면 부호 비트 s에 따라 양수 혹은 음수 무한대를 의미한다.
- e=255 AND f != 0 이면 NaN이다.
단정도 부동소수점이 표현 가능한 범위는 10진수로 다음과 같다.

10자리 이진수와 3자리 10진수는 비슷한 값을 갖는다.
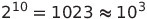
따라서 단정도 부동소수점은 사용하는 24bit 2진수는 일곱 자리 10진수와 비슷하므로 그만큼의 정밀도를 가진다고 생각할 수 있다. 하지만, 이는 틀린 말이다. 부동소수점은 지수부 값에 따라 달라진다. 즉, 단정도 부동소수점은 1/2^24 = 1/16,777,216 약 6/100,000,000 만큼의 정밀도를 가진다. 따라서 16,777,216과 16,777,217과 16,777,216.5를 구분하지 못하고 같은 단정도 부동소수점으로 저장된다. 그 때문에 돈을 다루는 등 정밀한 수치가 요구되면 고정 소수점을 사용한다. 또 한, 연산 결과가 정확하지 않는 문제도 발행한다. 예를 들어 연산 결과로 3.50을 기대했지만, 실제 결과는 3.49999999... 가 나오는 식이다. 이는 결과가 무한소수, 순환소수 등 가수부가 표현할 수 있는 범위를 초과했을 때 손실이 발생하기 때문이다.
배정도 표기법(double-precision)
단정도 표기법으로 원하는 만큼의 소수점 표현이 안된다면, 배정도 부동소수점을 사용하면 된다. 배정도 부동소수점 형식은 다음과 같다.

배정도 표기법은 편향 치로 1023을 사용하므로 다음과 같은 식으로 위 형식을 해석할 수 있다.
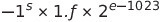
배정도 표기법도 단정도 표기법과 비슷하게 0, 무한대, NaN을 표기한다.
배정도 부동소수점의 범위는 10진수로 다음과 같다.