1.12 회로 기호도
논리 연산은 하드웨어, 소프트웨어 모두에서 수행할 수 있다. 소프트웨어에서 수행하는 논리 연산은 프로그래밍 언어 등에 내장된 기능을 사용하므로 이름과 기술에 따라 천차만별하다. 그에 반해 하드웨어의 경우 여러 기관에서 만든 회로도 기호가 존재하며 제조사, 국적과 관련 없이 이 기호들을 사용한다.
1.13 논리 연산의 응답 속도
상상과는 달리, 실제 하드웨어나 소프트웨어의 구현은 지연이 발생한다. 하드웨어에는 전기가 흐르는 시간이 존재해 이보다 빠르게 전기를 흘릴 수 없다. 또 한, 회로를 만드는 방식에 따라서도 속도 차이가 발생한다. 따라서 비록 등가 회로라고 해도, 정보가 전달되는 방식(전력, 속도 등)이 맞지 않으면 실제로 사용할 때 등가가 되지 않을 가능성이 존재한다.
예를 들어 아래의 두 회로는 모두 논리적 반적을 구현한 것이다. 하지만, 전력이나 속도 지연 측면에서는 서로 다르다.

1.14 음의 논리 출력 게이트
실제로 양의 논리 입력, 음의 논리 출력 게이트가 많이 존재한다. 입력과 출력에서 논리가 반대고, 결과가 옳다면 상관없고, 이런 방식을 채택하는 것이 부품을 줄일 수 있기 때문이다.
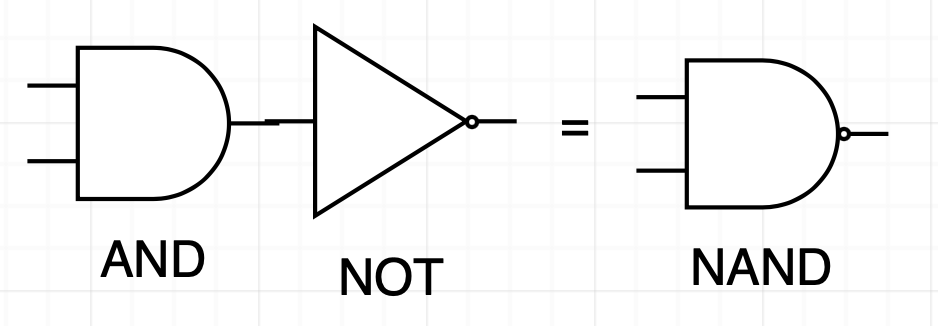
양의 논리 입력, 음의 논리 출력 AND를 NAND라 한다.
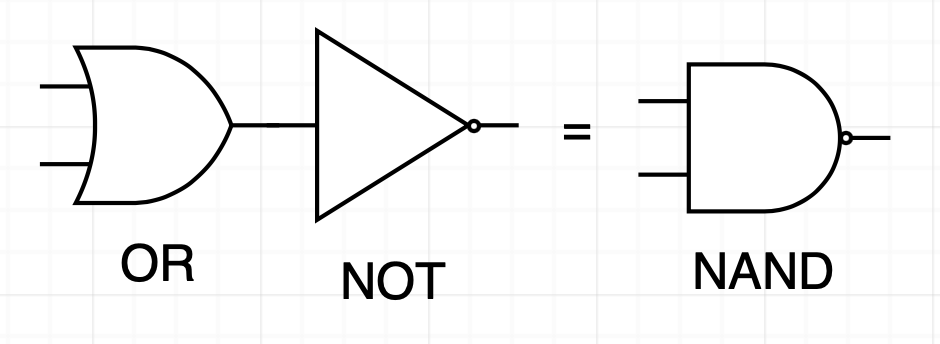
양의 논리 입력, 음의 논리 출력 OR을 NOR라 한다.
1.15 음의 논리 입력 게이트
음의 논리 입력, 양의 논리 출력 게이트는 존재하지 않는다. 등가 게이트를 쉽게 구현할 수 있기 때문이다.
- 음의 논리 입력, 양의 논리 출력의 AND -> NOR과 등가
- 음의 논리 입력과 양의 논리 출력의 OR -> NAND의 등가
음의 논리 입력, 음의 논리 출력 게이트 역시 등가 게이트를 간단히 구할 수 있다.
- 음의 논리 입력과 음의 논리 출력의 AND -> OR과 등가
- 음의 논리 입력과 음의 논리 출력의 OR -> AND의 등가
1.16 다입력 게이트
AND 게이트와 OR 게이트의 입력은 두 개로 제한돼 있지 않다. 원하는 만큼 늘릴 수 있다. 이때, 각 게이트는 다음과 같은 규칙을 갖는다.
- 다입력 AND 연산 - 모든 입력이 참이면 결과도 참
- 다입력 OR 연산 - 최소 하나의 입력이 참이면 결과도 참
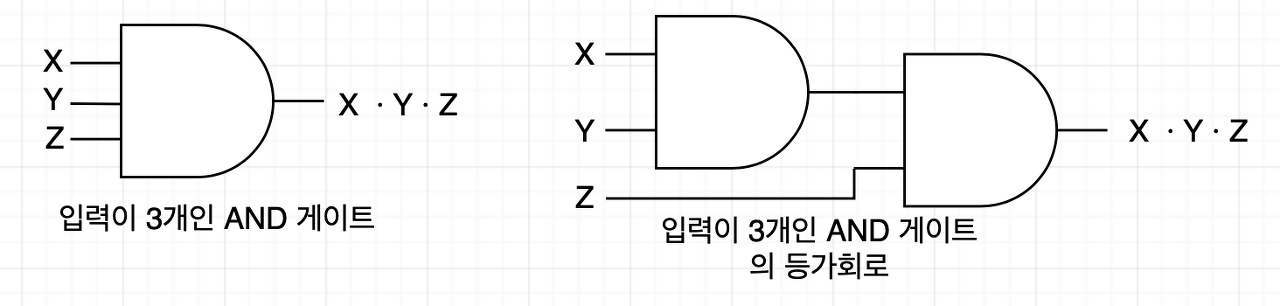
입력이 3개인 AND 게이트와 입력이 더 적은 AND 게이트를 여러 개 조합해 만든 등가 회로는 다음과 같다.
1.17 수치의 기저
컴퓨터가 사람과 달리 숫자를 0부터 세는 이유는 효율적이기 때문이다. 하지만 일부 프로그래밍 언어의 경우 숫자를 1부터 세는 기능을 지원한다. 예를 들어 BASIC 언어의 Option Base문은 배열의 인덱스를 1로 할지, 0으로 할지를 정할 수 있다.
더 자세한 내용은 Why numbering should start at zero를 참고하자.
출처 - 성공과 실패를 결정하는 1%의 프로그래밍 작동 원리