1.6 조지 부울의 등장
조지 부울은 모든 논리는 0과 1의 두 값으로 환원할 수 있다는 논리를 발표했고 이를 부울 대수라 부른다. 부울 대수는 컴퓨터에는 왜 True(1), False(0)만 표현할 수 있는 2치 논리형이 좋은가의 논리적 근거가 된다.
조지 부울이 밝힌 논리를 실제의 전기 회로로 실현한 것이 논리 회로이며 대부분의 디지털 회로가 논리회로다.
논리 회로로 인해 다음과 같은 것들이 가능해졌다.
1. 계산
2. 기억
3. 사례 구분
4. 카운터
5. 선택
1.7 비트
대부분의 컴퓨터는 디지털 방식으로 동작한다. 데이터는 2치 논리형으로 취급된다. 컴퓨터 내부 정보를 더 이상 나눌 수 없는 최소의 상태까지 나누면 False, True가 된다. 이 최소 단위를 비트라 한다.
비트를 표현하는 방식에는 여러 가지가 있지만 결론적으로 "있음", "없음"만 구별할 수 있으면 된다.
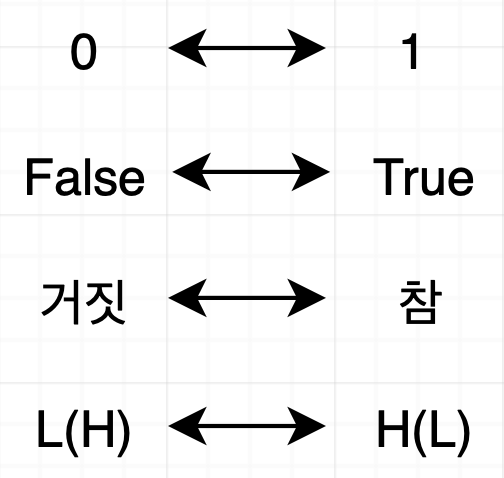
많은 컴퓨터 언어들의 명세에선 0 이외의 모든 수를 True로 간주하고 있다. 이렇게 되면 두 값이 일치하는지를 비교할 때 의도한 대로 동작하지 않는 문제가 발생한다. 이 문제를 C언어 예시로 들면 다음과 같다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
#include <stdio.h>
int main(void) {
int a = 1;
int b = 2;
if (a) printf("a is true.\n");
if (b) printf("b is true.\n");
if (a == b) printf("a and b are the same.\n");
else printf("a and b are different.\n");
}
// 결과
// a is true.
// b is true.
// a and b are different.
|
cs |
하지만 이 문제가 그리 심각하진 않다. 그저 틀린 질문이 거짓이 되는 정도의 문제다.
위에서 서술한 비트 구별 기호 중 L(H)는 False가 L 또는 H, True가 H 또는 L로 표현되는 것을 의미한다.
1.8 전압과 비트
전선을 접속해 비트를 보낼 때 비트 구분을 어떻게 할 것인가 라는 문제가 발생한다. 비트 구분을 하는 방식은 다음과 같다.
1. 전류가 흐름 <-> 전류가 흐르지 않음
2. 전압이 높음 <-> 전압이 낮음
3. 주파수가 높음 <-> 주파수가 낮음
이 중 위에서 언급한 L(H), H(L) 비트 구별 기호는 전압의 높음/낮음으로 비트를 식별하는 경우다. 여기서 비트를 낮은 쪽을 True로 할지, 높은 쪽을 True로 할지에 대한 문제가 나타난다. 전원이 높은 쪽을 True로 간주하는 회로 설계를 양의 논리, 전원이 낮은 쪽을 True로 간주하는 회로 설계를 음의 논리라 한다. L(H)는 음의 논리, H(L)은 양의 논리를 의미한다.
하나의 회로 안에 음의 논리와 양의 논리가 모두 혼재한 경우도 존재한다. 하지만 다음과 같이 아무런 조치도 취하지 않을 경우 오작동이 발생한다.
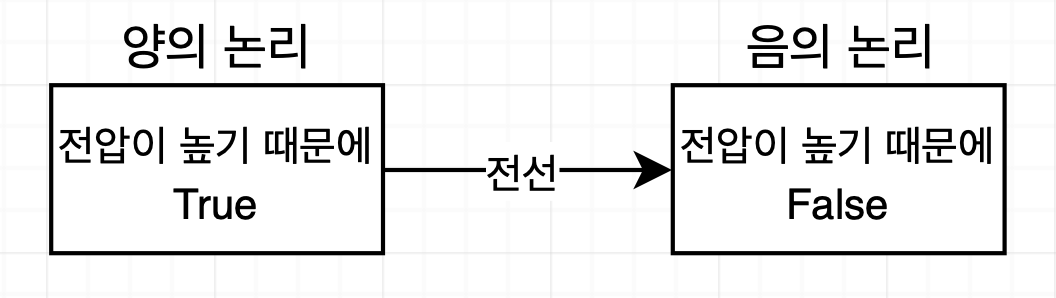
하지만 등가회로의 경우 혼재를 허용해도 문제가 발생하지 않는다. 등가 회로는 이름에서 알 수 있는 같은 결과(가치)가 같은 회로를 의미한다. 즉, 음의 논리와 양의 논리를 이용해 산출한 결과가 같다는 것을 의미한다.
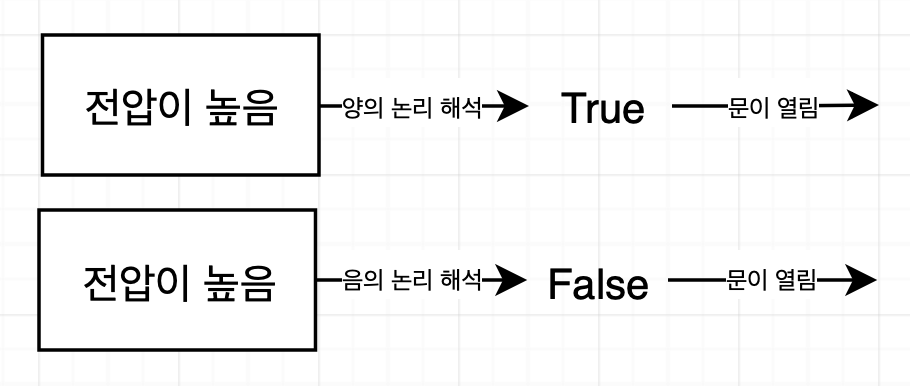
결과가 동일한 값을 가지면, 회로를 어떤 방식으로 해석하던 상관없다. 따라서 결과가 동일하는 한, 기능이 다른 별도의 부품으로 교체해도 된다. 이를 이용해 기능은 동일하나 부품 수가 훨씬 적은 회로를 작성할 수도 있다.
만약 등가 회로를 구성할 수 없는 경우 양의 논리와 음의 논리 중간에 NOT 연산을 행하는 장치를 두면 된다.

출처 - 성공과 실패를 결정하는 1%의 프로그래밍 작동 원리