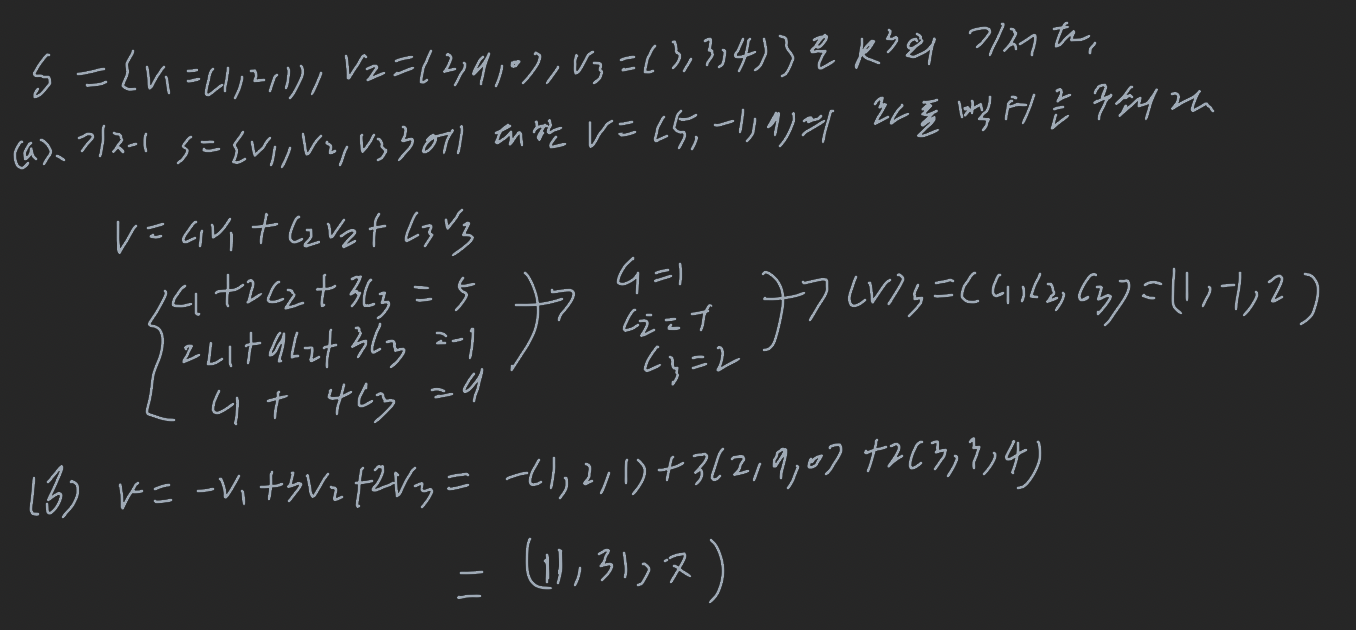벡터 공간의 기저(좌표계의 개념을 일반 벡터 공간으로 확장)
벡터 공간 V가 유한개의 벡터에 의해 생성된다면 유한차원이라 하고, 그런 집합이 존재하지 않으면 무한차원이라 한다.
정의1.
만약 V가 임의의 벡터공간이고 S = {v1, v2, .., vn}이 벡터 V안의 유한 집합이라면, s다 다음 두 조건을 만족할 때 V의 기저라 한다.
1. s는 일차독립
2. s는 V를 생성한다.
기저: 벡터 공간을 생성하는 최소한의 벡터 모임

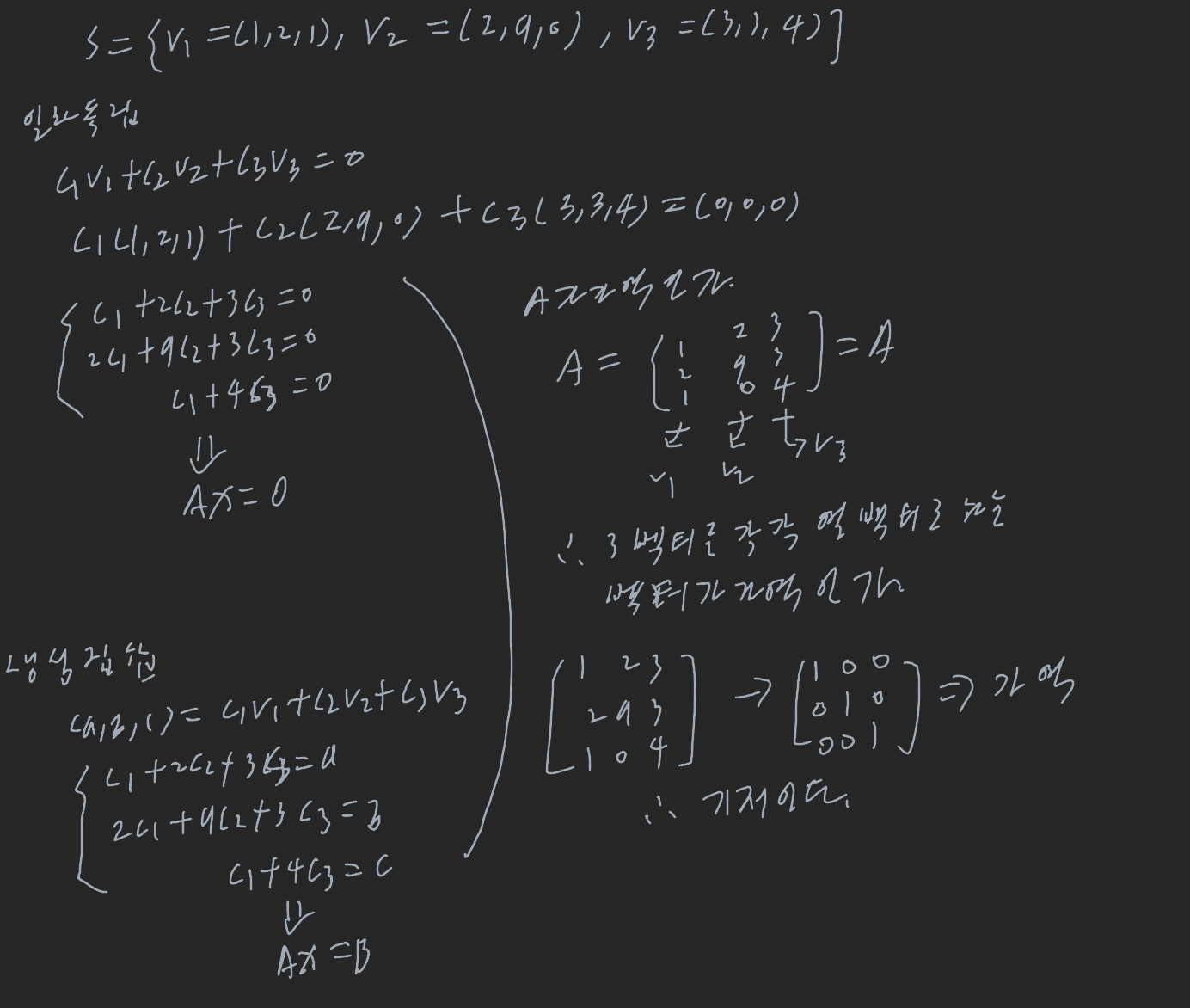
좌표
s = {v1, v2, ...., vn}이 벡터공간 V의 기저라 하자. 그러면 V속의 모든 벡터 V는 단 한가지 방법
V = c1v1+ c2v2+ ....+ +cnvn
으로 표현된다.
s = {v1, v2, ...., vn}이 벡터공간 V의 기저이고,
V = c1v1+ c2v2+ ....+ +cnvn
이 기저 s를 이용한 V의 표현일 때, 스칼라 c1, c2, ..., cn을 기저 S에 대한 V의 좌표 라 한다. 이들 좌표로 구성된 R^n의 벡터(c1, c2, ..., cn)를 기저 S에 대한 V의 좌표벡터라 하고
(V)s = (c1, c2, ...., cn)
으로 표기한다.