일차 독립과 일차 종속
S = {v1, v2, .., vr}가 벡터공간 V의 두 개 이상의 벡터들의 집합이고 S의 어떤 벡터도 다른 벡터의 선형결합으로 표현될 수 없다면, S는 선형독립집합(linearly independent set)이라 한다. 선형독립이 아닌 집합은 선형종속집합(linearly dependet ste)이라 한다. 만약 집합 S가 단 하나의 벡터로 구성된다면 그 집합이 선형독립이기 위한 필요충분조건은 그 벡터가 영벡터가 아닌것이다.
벡터집합의 선형독립여부 확인
벡터공간 V의 공집합이 아닌 집합 S가 선형독립이기 위한 필요충분조건은 벡터방정식
k1v1 + k2v2 + .... + krvr = 0
을 만족시키는 계수가 k1 = 0, k2 = 0, ..., kr = 0인 것이다(자명해가 나온다면 선형종속이다.)
ex)

두개의 벡터를 가진 집합과 영벡터를 포함하는 집합의 선형독립
1. 영벡터를 포함하는 유한집합은 일차종속이다
2. 두 벡터만을 갖는 집합이 일차독립이기 위한 필요충분조건은 이들 벡터 중의 어느 벡터도 다른 벡터의 스칼라배로 되지 않는 것이다.
일차독립의 기하적 해석:
1. R^2와 R^3에서 두 벡터가 일차 독립일 필요충분 조건은 이들 벡터의 시점이 원점에 위치해 있을때 동일 직선상에 있지 않는 것이다.
3. R^3의 세 벡터가 일차독립일 필요충분조건은 이들 벡터의 시점을 원점에 두었을때 동일 평면상에 있지 않는 것이다.
정리:
S = {v1, v2, ..., vr}이 R^n상의 벡터의 집합이라 하자, 만약 r > n이면, S는 일차종속이다.
정의
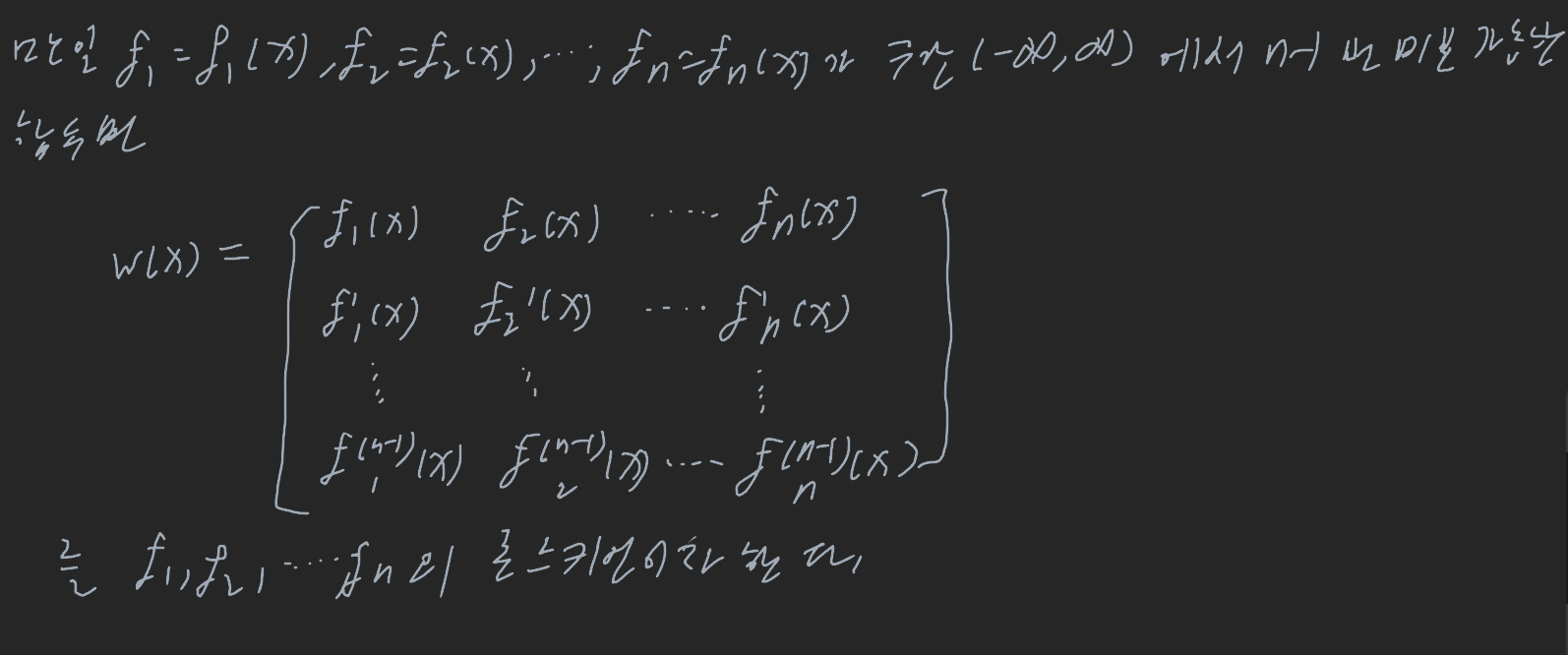
만일 f1, f2, ..., fn가 구간 (-♾,♾)에서 n - 1차 연속함수를 가지고, 이들 함수의 론스키언이 (-♾, ♾)의 모든 x에 대해 항상 영이지 않는다면, 이들 함수는 C^(n - 1)(-♾, ♾)의 벡터의 일차독립집합을 이룬다.