n차원 벡터 공간 R^n에서 벡터의 대수적 기본 성질을 공리로 이용해 벡터개념을 확장해 일반벡터공산을 구성한다.
벡터공간의 공리
V를 두 연산 덧셈과 스칼라곱셈이 정의되는 개체들의 집합이라 하자. V는 공집합이 아니라고 가정한다. 여기서 덧셈(addition)이란, V의 임의의 한 쌍의 개체 u, v에 대해 u와v의 합(sum)이라 불리는 개체 u+v를 연관시키는 규칙을 뜻한다. 또한, 스칼라곱(scalar multiplication)이란, V의 임의의 개체u와 임의의 스칼라 k에 대해 스칼라배(scalar multiple)라고 불리는 개체 ku를 연관시키는 규칙을 뜻한다. 다음 모든 공리가 V의 모든 개체 u, v와 모든 스칼라 k, m에 대해 만족될 때, V를 벡터공간(vector space)이라 하고 V의 개체를 벡터(vector)라 부른다.
공리:
1. u, v가 V의 개체이면 u + v도 V에속한다(덧셈에 대한 닫힘성)
2. u + v = v + u
3. (u + v) + w = u + (v + w)
4. V의 모든 u에 대해 u + 0 = 0 + u = u를 만족하는 개체 0이 V에 존재한다. 이것을 V의 영벡터(zero vector)라고 부른다
5. V의 모든 u에 대해 u + (-u) = (-u) + u = 0을 만족하는 개체 -u가 V에 존재한다. 이것을 u의 음(negative of u)라 부른다.
6. k가 임의의 스칼라이고 u가 V의 개체이면 ku는 V에 속한다(스칼라곱에 대한 닫힘성)
7. k(u + v) = ku + kv
8. (k + m)u = ku + mu
9. k(mu) = (km)u
10. 1u = u
종류의 개체가 벡터가 될 수 있고, 벡터 공간의 연산은 반드시 모든 R^n에서의 덧셈과 스칼라 곱셈일 필요는 없다. 단지 벡터 공산의 10개 공리를 만족하면 된다.
두 연산을 가진 집합이 벡터공간임을 보이기
1. 벡터가 될 개체의 집합 V를 식별한다
2. V상의 덧셈과 스칼라 곱셈 연산을 식별한다
3. 공리1과 6을 검증한다. 즉, V의 두 벡터를 더하면 V의 벡터가 되고, V의 한 벡터에 스칼라를 곱해도 V의 벡터가 됨을 보인다. 공리 1을 덧셈에 대한 닫힌 성질, 공리 6을 스칼라곱셈에 대한 닫힌 성질이라 한다.
4. 그 외 공리들이 성립함을 보인다.
예제:
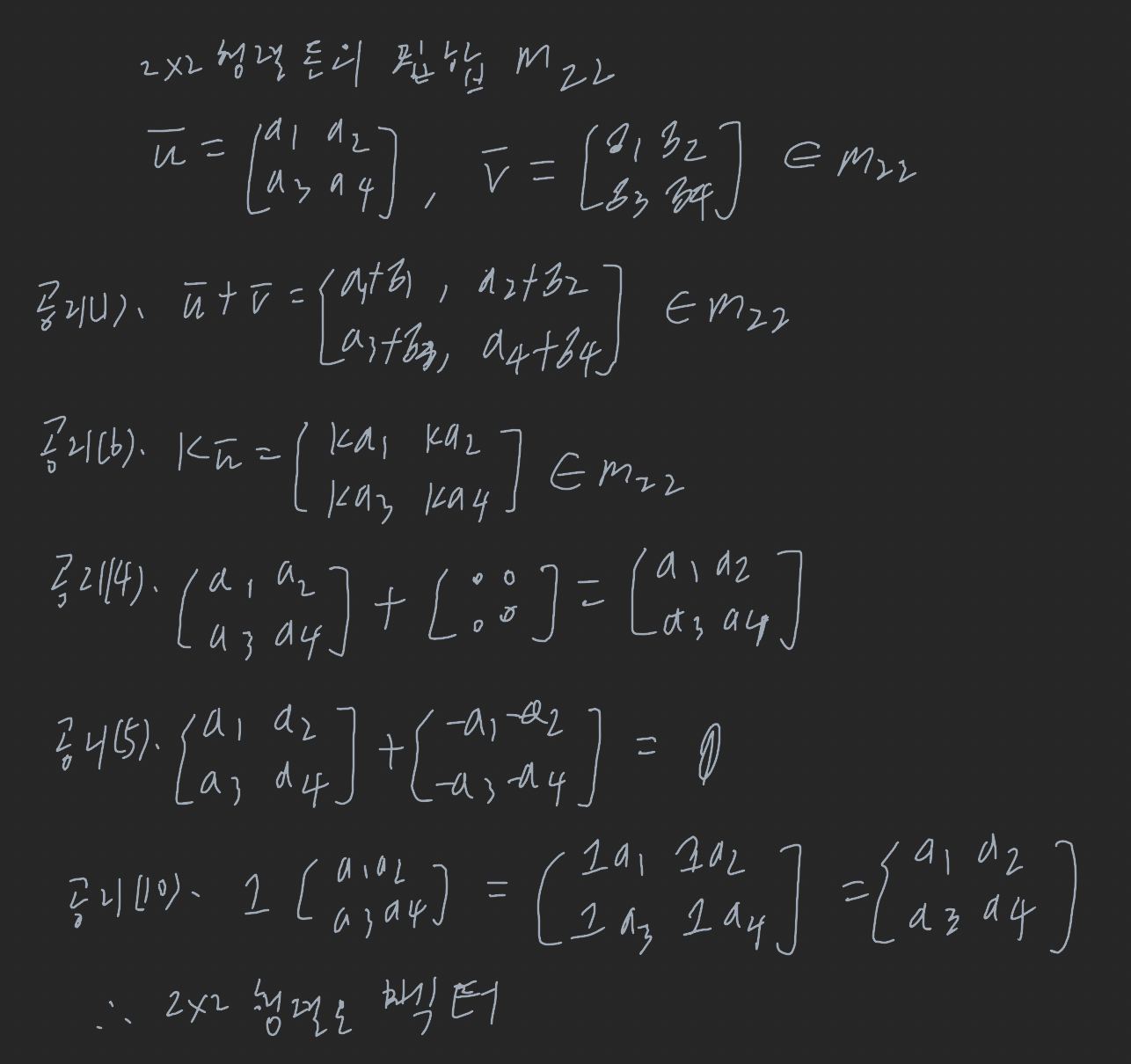
정리: V는 벡터공산, u는 V의 벡터, k는 스칼라할떄
1. 0u = 0
2. k0 = 0
3. (-1)u = -u
4. 만약 ku = 0이면, k = 0이거나 u = 0