두 영이 아닌 벡터 u, v사이의 각은 다음과 같이 정의된다.
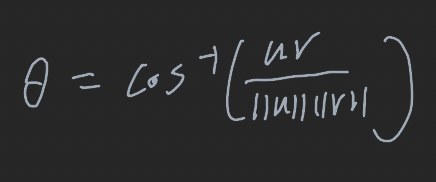
이 정의에서 ⍬ = π/2이기 위한 필요충분 조전은 uv = 0이므로 다음과 같은 정의를 얻는다.
두 영이 아닌 R^n벡터, u,v에 대해 uv = 0이면 u,v는 서로 직교한다. 또 한 R^n의 영벡터는 모든 R^n벡터에 직교한다. 공집합이 아닌 R^n의 벡터들의 집합에서 안에 있는 모든 서로 다른 두 벡터들이 직교하면, 이것을 직교집합이라 한다. 또 한 단위 벡터들의 직교집합을 정규직교집합이라 한다.
점과 법선벡터에 의해 결정되는 직선과 평면
1. a, b가 상수이고 모두 영이 아니면, 방정식
ax + by + c = 0
은 n = (a, b)을 법선벡터로 갖는 R^2의 직선을 나타낸다, 원점을 지나는 방정식은 ax + by = 0
2. a, b, c가 상수이고 모두 영이 아니면, 방정식
ax + by + cz + d = 0
은 n = (a, b, c)을 법선벡터로 갖는 R^3의 평면을 나타낸다, 원점을 지나는 방정식은 ax + by + cz = 0
정사영
사영 정리
u와 a가 R^n벡터이고 a != 0이면, u는 u = w1 + w2의 형태로 유일하게 표현할 수 있다. 여기서 w1은 a의 스칼래 배이고 ws는 a에 수직인 벡터이다.

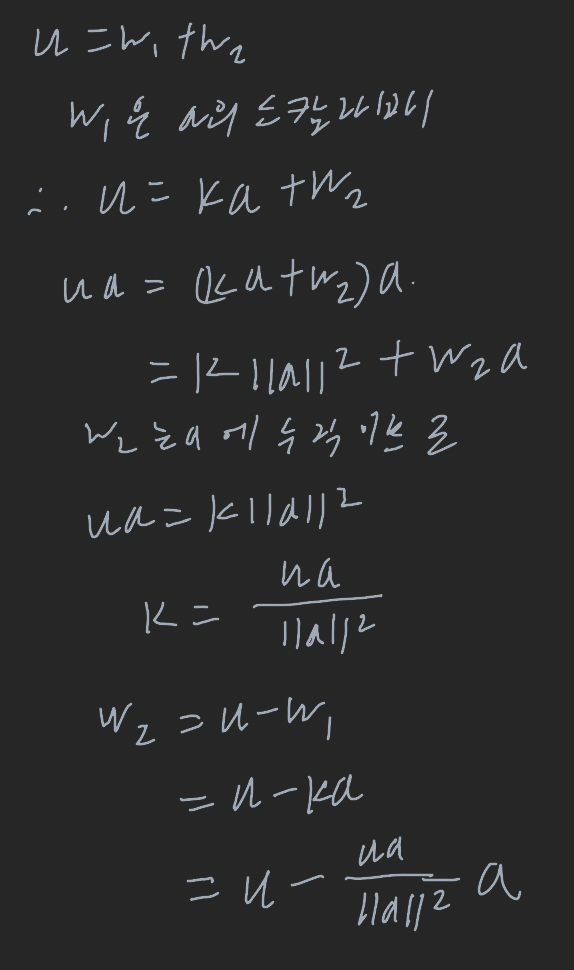
이때 사영정리에 있는 벡터 w1, w2에 대해서 w1을 u의 a로의 정사영 또는 u의 a방향의 벡터성분이라 하고, w2를 u의 a에 직교하는 벡터성분이라 한다. w1을 다음과 같이 표기하고

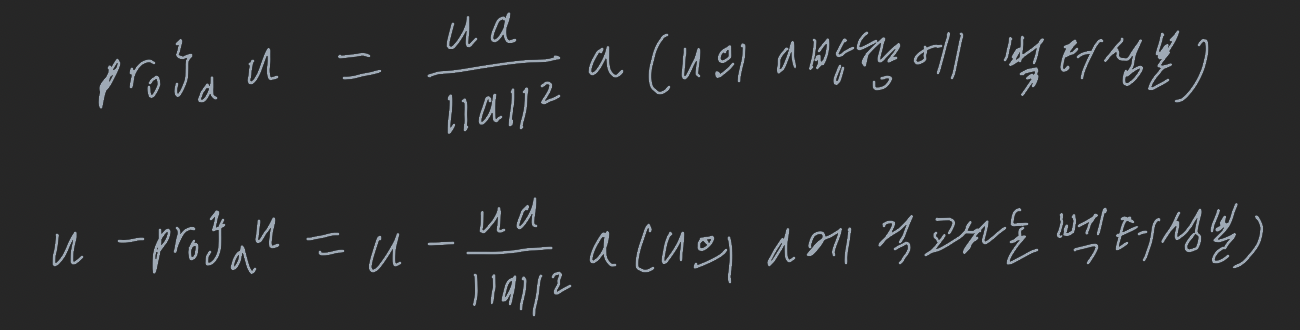
U의 a방향의 벡터성분의 크기
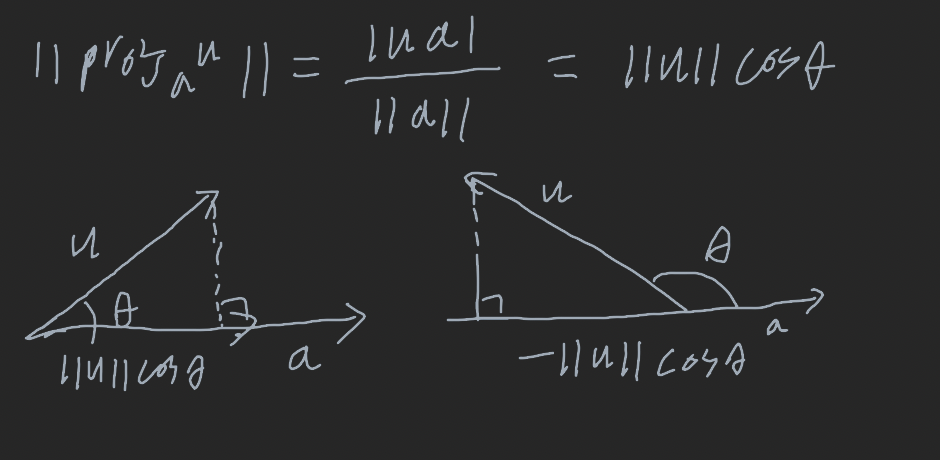
피타고라스의 정리
u, v가 유클리드 내적에 대해 R^n의 직교하는 벡터이면
||u+v||^2 = ||u||^2 + ||v||^2