벡터의 놈
벡터 v의 길이를 놈이라 하고 ||v||로 나타낸다.
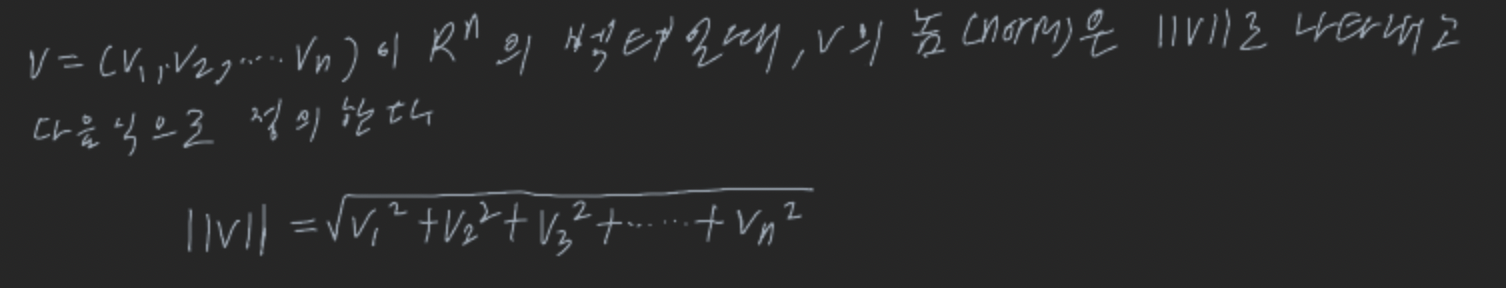
정리: v가 R^n의 벡터익고 k가 임의의 스칼라이면
1. ||v|| >= 0
2. ||v|| = 0이기 위한 필요충분조건은 v=0이다
3. ||kv|| >= |k| ||v||
단위 벡터
놈이 1인 벡터를 단위벡터라 한다. 단위 벡터를 어더기 위해 영이 아닌 벡터를 자신의 길이의 역수를 곱하는 과정을 v의 정규화라고 한다.
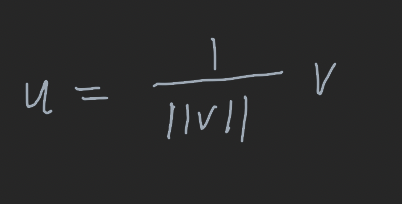
위 식은 v와 같은 방향의 단위벡터이다.
표준 단위 벡터
R^n의 표준단위 벡터들은 다음과 같이 정의한다.

R^n의 모든 벡터 v=(v1, v2, ...., vn)는

R^n에서의 거리
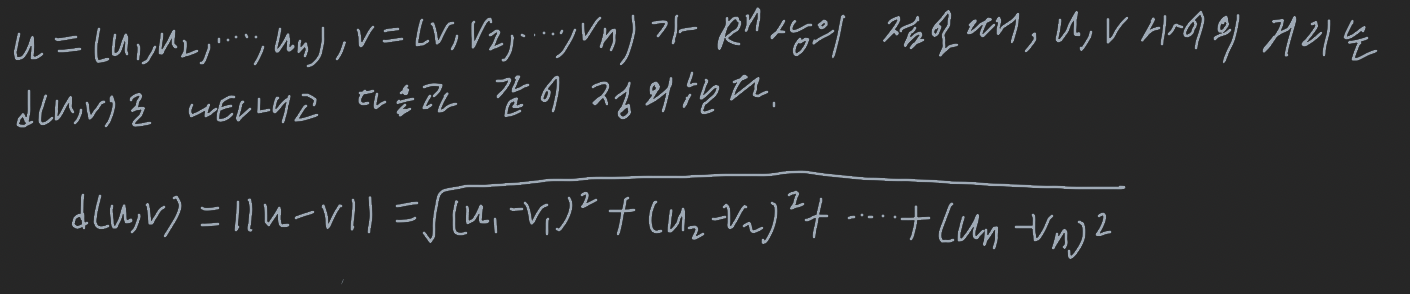
점곱



점곱의 대수적 성질
R^n벡터 u, v, w와 스칼라 k에 대해 다음과 같은 성질이 성립한다
1. uv=vu
2. u(v+w) = uv + vw
3. k(uv) = (ku)v
4. vv >= 0이고 vv = 0이기 위한 필요충분 조건은 v = 0이다.
5. Ov = vO = 0
6. (u+v)w = uw + vw
7. u(v-w) = uv - uw
8. (u-v)w = uw - vw
9. k(uv) = u(kv)
코시-슈바르츠 부등식
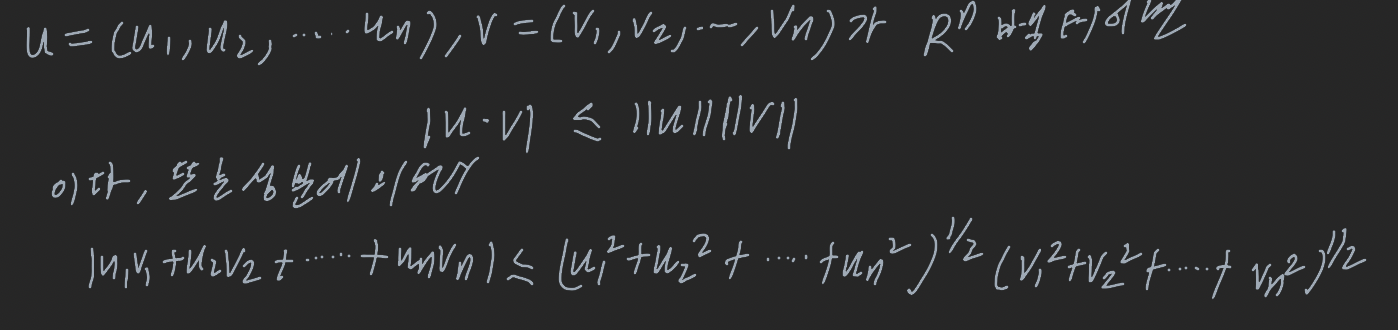
정리: R^n의 벡터 u, v, w와 스칼라 k에 대해
1. ||u+v|| <= ||u|| + ||v||
2. d(u, v) <= d(u, w) + d(w, v)
벡터의 평행 사변형 등식
R^n의 벡터 u, v에 대해
||u + v||^2 + ||u - v||^2 = 2(||u||^2 + ||v||^2)
R^n의 벡터, u, v는 유클리드 내적에 대해 다음을 만족한다
uv = 1/4||u + v||^2 - 1/4||u - v||^2