행렬의 성질 1: det(kA) = k^n det(A)
정리 2.3.1:
A, B, C가 제 r행 한 행만 다른 n*n행렬이라 하자. C의 제 r행은 A, B의 제 r행의 대응하는 원소들을 더하여 얻어진 것이라 가정하면
det(C) = det(A) + det(A)
이고 이는 열에 대해서도 성립한다.
정리 2.3.2:
만약 A, B가 같은 크기의 정방행렬이면
det(AB) = det(A)det(B) 이다
정리 2.3.3:
정방행렬 A가 가영이기 위한 필요충분 조건은 det(A) != 0이다
정리 2.3.4:
A가 가역이면 det(A^-1) = (det(A))^-1이다
딸림 행렬

딸림 행렬을 이용한 역행렬 구하기
A가 가역이면 A^-1 = 1/det(A) * adj(A)
정리 2.3.7 크라머의 규칙
Ax=b가 n개의 미지수, n개의 일차방정식으로 이루어진 연립일차방정식이고 det(A) != 0이면, 연립방정식은 유일한 해를 갖는다, 해는
x1 = det(A1)/det(A), x2 = det(A2)/det(A), ....., xn = det(An)/det(A)
여기서 Aj는 A의 j번째 열의 원소를 행렬
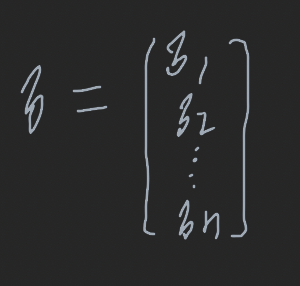
의 원소로 대체해 얻은 행렬이다