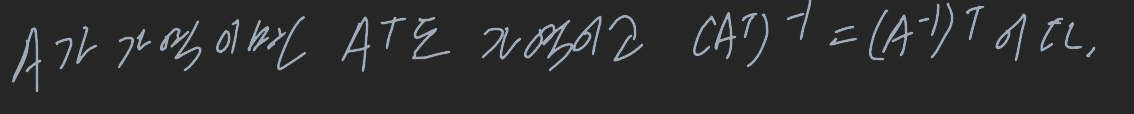행렬 곱셈에서는 순서가 중요하다. AB != BA
영행렬 - 모든 원소가 0인 행렬, 영행렬은 0으로 표기한다.

단위 행렬
주대각선 상의 원소들은 1이고 나머지 원소들은 모두 -이면 이런 행렬을 단위행렬(unit matrix) 또는 항등행렬(identity matrix)라 한다.

단위행렬은 I로 표시한다. 크기를 강조할때는 n x n단위 행렬응ㄹ In으로 표시한다.
정리 만약 R이 n x n행렬 A의 기약 행사다리꼴이면 R은 0으로만 된 행을 갖든가 아니면 행렬 In이다.
역행렬
정의 1. 만약 A가 정방행렬이고 AB = BA = I를 만족하는 같은 크기의 B가 존재한다면 A는 가역(inventible) 또는 정칙(nonsigular)이라 하고 B를 A의 역행렬(inverse)라 한다. 만약 그와 같은 행렬 B가 존재하지 않으면 A는 특이행렬(singular)이라 한다.

위 예제에서 A, B는 가역이고 서로가 서로에게 역행렬이 된다.
정리 1.4.5. B와 C가 모두 A의 역행렬이면 B = C이다.
A가 가역이면 그것의 역행렬은 A^(-1)이다. 그러므로 AA^(-1)=I, A(-1)A=I

역행렬로 연립일차 방정식의 해 구하기

정리 1.4.6 만약 행렬 A와 B가 같은 크기의 가역 행렬이면 AB는 가역이고 (AB)^-1 = B^-1 A^-1이다.
어떠한 가역 행렬들의 곱도 가역이며 그 곱의 역행렬은 각각의 역행렬을 역순으로 곱하여 얻을 수 있다.
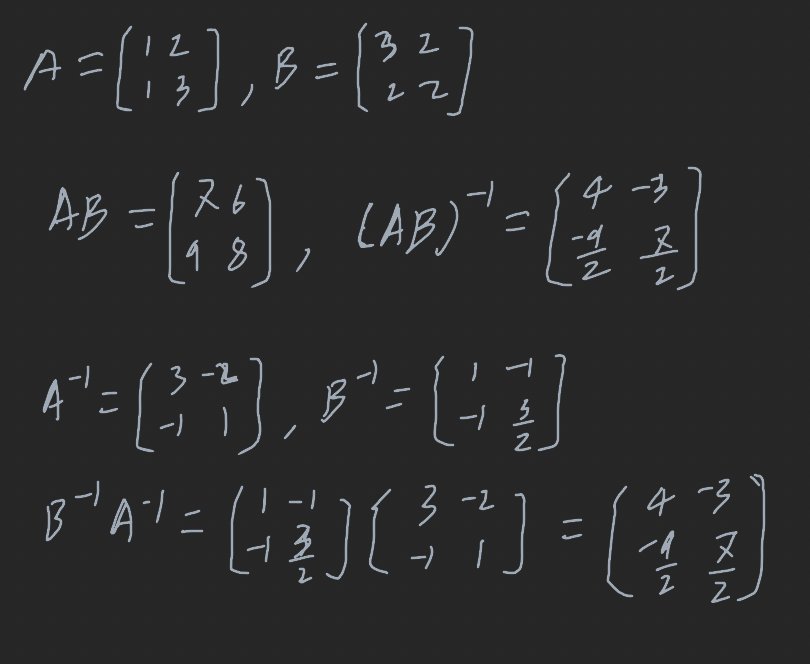
행렬의 거듭제곱
만약 A가 정방행렬이면 A의 음이 아닌 정수에 대한 거즙제곱은 다음과 같이 정의한다.

그리고 A가 가역이면 A의 음의 정수에 대한 거듭제곱도 다음과 같이 정의한다

실수와 마찬가지로 정의되므로 음이 아닌 지수에 대한 법칙들도 성립한다.

또 한 음의 지수에 대해 다음 성질을 얻는다
정리 1.4.7 행렬 A가 가역이고 n이 음이 아닌 정수라 하자
1. A^-1도 가역이고 (A^-1)^-1=A이다
2. A^n도 가영이고 (A^n)^-1 = A^-1 = (A^-1)^n
3. 임의의 0이 아닌 스칼라에 대해서 kA도 가역이고 (kA)^-1=k^-1A^-1 이다.
행렬 합의 제곱
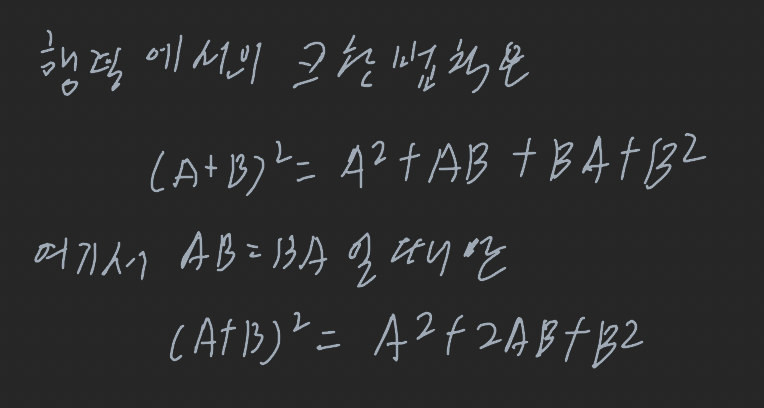
행렬다항식

전치행렬의 성질