정의 1. 행렬은 숫자들의 직사각형 배열이디. 배열 안에 있는 숫자들을 행렬의 우너서라 한다.
행렬의 크기는 행과 열의 개수로 표현한다(mXn). 행렬을 말할때 보통 숫자를 스칼라 라고 한다. 이때 스칼라는 실수를 의미한다.
행벡터는 행이 1개, 열벡터는 열리 1개인 것을 의미한다. n*n크키를 가진 행렬을 n의 정방행렬(square matrix)라 한다. 정방행렬에서 a11, a22, ... ann은 A의 주대각선(main diagonal)상에 있다고 한다.
정의 2. 두 행렬의 크기가 같고, 서로 대응되는 원소가 같으면 두 행렬이 같다.

정의 3. 행렬 A와 B의 크기가 같으면 합 A+B는 B의 원소에 대응되는 A의 원소를 더하여 얻을 수 있고 차 A-B는 A의 원소에 대응되는 B의 원소를 빼서 얻을 수 있다. 다른 크기의 생렬들은 더하거나 뺄 수 없다.
정의4. A를 임의의 행렬, c를 임의의 스칼라라고 하면 곱 cA는 행렬 A의 모든 원소에 스칼라 c를 곱하여 얻어진다. 행렬 cA를 A의 스칼라곱이라고 한다.
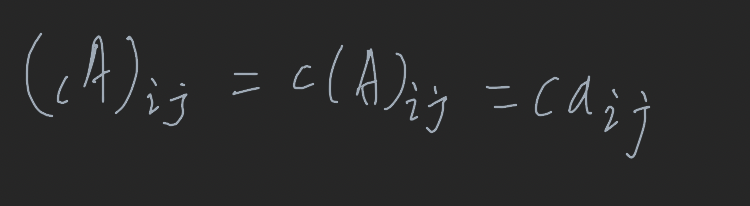
정의 5. A가 n x m행렬이고 B가 r x n행렬이면 곱 AB는 m x n행렬이고 그것의 원소는 다음과 같이 결정된다: AB의 i행과 j열에 있는 원소는 행렬 A의 i행과 행렬 B의 j열에 있는 대응되는 원소들의 곱을 더해서 얻어진다.
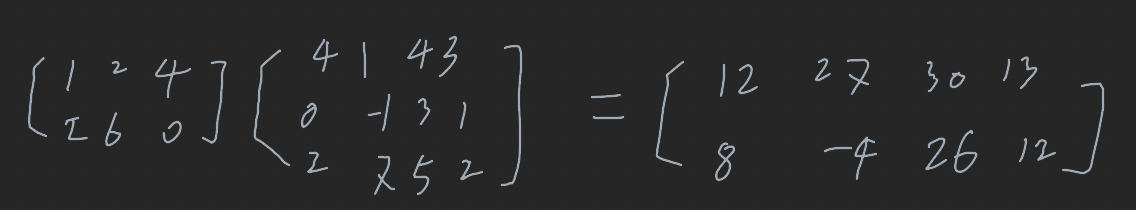
분할된 행렬
행렬은 선택된 행과 열 사이에 수평선과 수직선을 넣어서 더 작은 행렬로 분할될 수 있다.
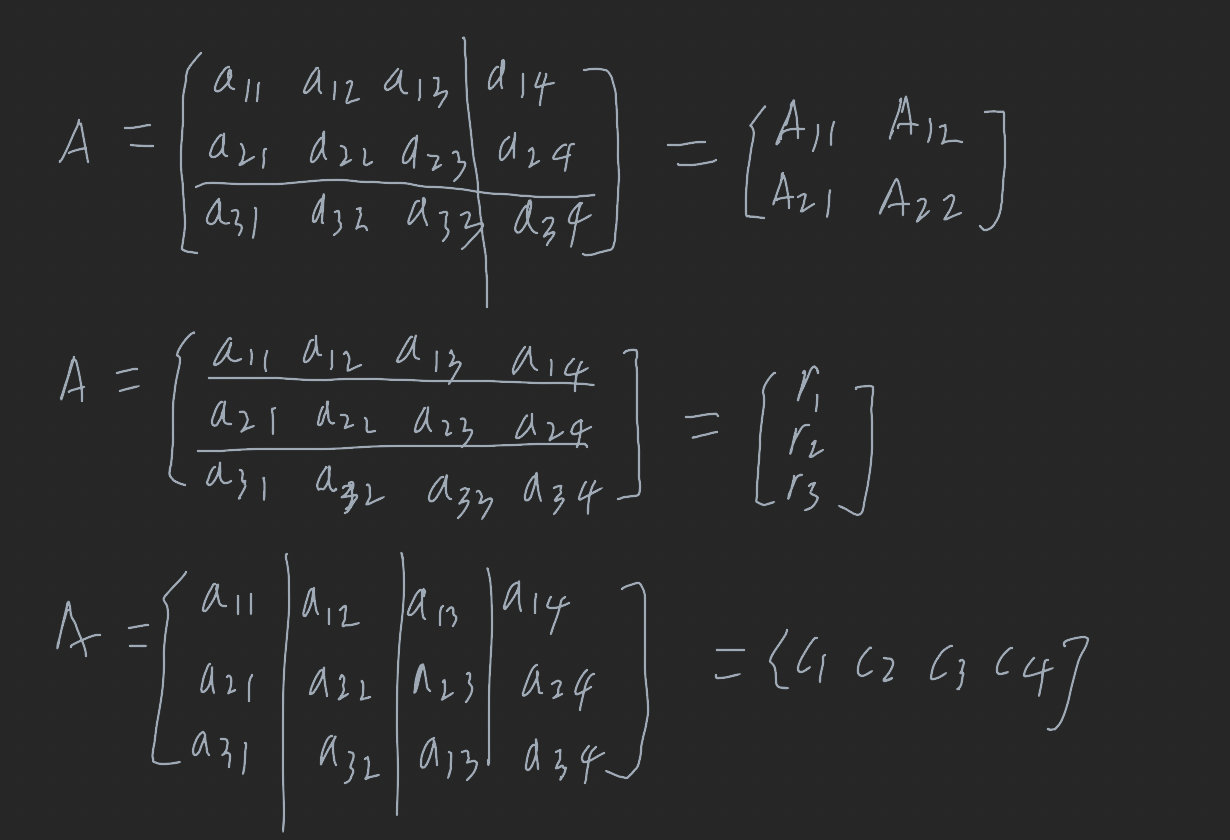
분할된 행렬은 행렬의 곱 AB의 특정한 행이나 열을 다 생각하지 않고 찾아낼 수 있다. AB의 각 열젝터들은 B를 열벡터로 분할해 곱하여 얻을 수 있고 AB의 각 행벡터는 A를 행벡터로 분할해 곱하여 얻을 수 있다.

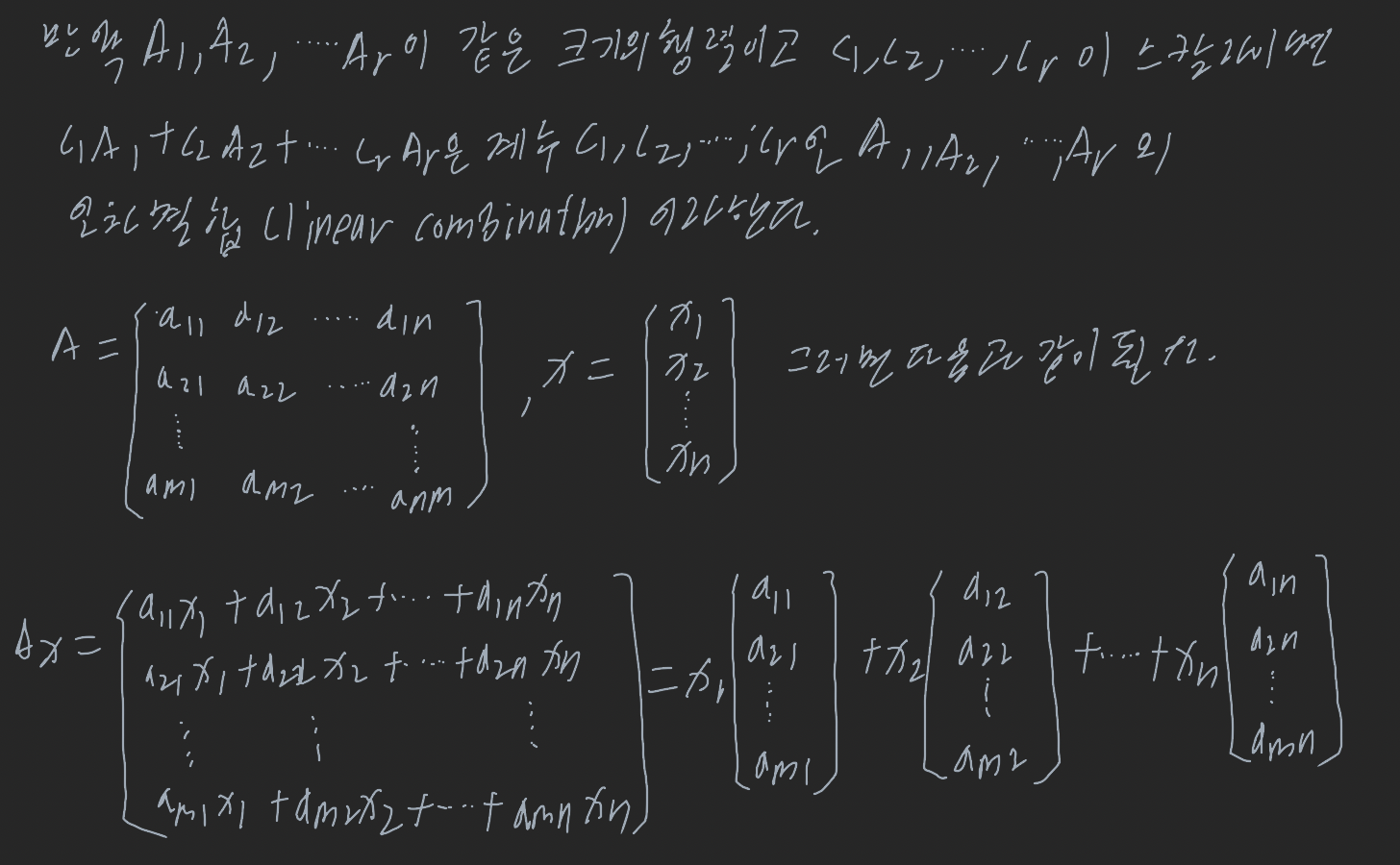
정리 1.3.1 만약 A가 m x n행렬이고 x가 n x 1열백터이면 곱 Ax는 계수가 x의 원소들인 A의 열벡터들의 일차결합으로 표현된다.
연립일차방정식의 행렬 형태
n개의 미지수와 m개의 방정식으로 이루어진 연립일차방정식을 살펴보자
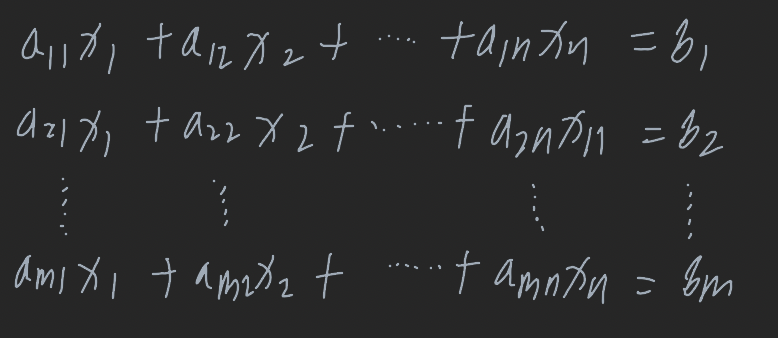
두 행렬이 같다는 것은 그들의 대응되는 원소들이 같다는 것이므로 m개의 방정식을 하나의 행렬 방정식으로 나타낼 수 있다.
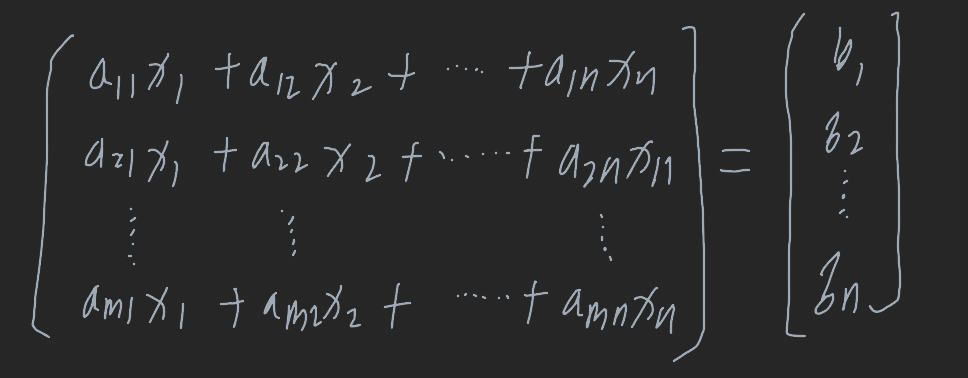
이들을 A, x, b로 나타내면

여기서 행렬 A를 계수 행렬(coefficient matrix)라고 한다. 이 연립방정식에서의 첨가행렬(argumented matrix)은 A에 b를 마지막 열로 첨가해 얻어진다. 즉, 첨가행렬은 다음과 같다

정의 7: A가 m x n행렬이면 A^T로 표시되는 A의 전치행렬은 n x m행렬이고 A의 행과 열을 바꾼 행렬이다.

A가 정방행령인 경우 A의 전치행렬은 주대각선을 중심으로 대칭 위치에 있는 원소들을 교환하여 얻을 수 있다.

정의 8 만약 정방행렬이면 A의 대각합(trace)은 tr(A)로 표기되고 A의 주대각선 상에 있는 원소들의 합으로 정의된다. A가 정방행렬이 아니면 A의 대각합은 정의되지 않는다.